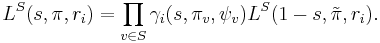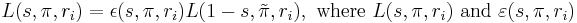Langlands–Shahidi method
In mathematics, the Langlands–Shahidi method provides the means to define automorphic L-functions in many cases that arise with connected reductive groups over a number field. This includes Rankin–Selberg products for cuspidal automorphic representations of general linear groups. The method develops the theory of the local coefficient, which links to the global theory via Eisenstein series. The resulting L-functions satisfy a number of analytic properties, including an important functional equation.
Contents |
The local coefficient
The setting is in the generality of a connected quasi-split reductive group  , together with a Levi subgroup
, together with a Levi subgroup  , defined over a local field
, defined over a local field  . For example, if
. For example, if 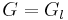 is a classical group of rank
is a classical group of rank 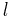 , its maximal Levi subgroups are of the form
, its maximal Levi subgroups are of the form 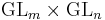 ,
, 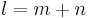 . F. Shahidi develops the theory of the local coefficient for irreducible generic representations of
. F. Shahidi develops the theory of the local coefficient for irreducible generic representations of 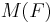 [1]. The local coefficient is defined by means of the uniqueness property of Whittaker models paired with the theory of intertwining operators for representations obtained by parabolic induction from generic representations.
[1]. The local coefficient is defined by means of the uniqueness property of Whittaker models paired with the theory of intertwining operators for representations obtained by parabolic induction from generic representations.
The global intertwining operator appearing in the functional equation of Langlands' theory of Eisenstein series[2] can be decomposed as a product of local intertwining operators. When  is a maximal Levi subgroup, local coefficients arise from Fourier coefficients of appropriately chosen Eisenstein series and satisfy a crude functional equation involving a product of partial L-functions.
is a maximal Levi subgroup, local coefficients arise from Fourier coefficients of appropriately chosen Eisenstein series and satisfy a crude functional equation involving a product of partial L-functions.
Local factors and functional equation
An induction step refines the crude functional equation of a globally generic cuspidal automorphic representation 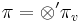 to individual functional equations of partial
to individual functional equations of partial  -functions and
-functions and  -factors[3]:
-factors[3]:
The details are technical: 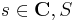 is a finite set of places (of the underlying global field) with
is a finite set of places (of the underlying global field) with 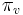 unramified for
unramified for 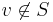 , and
, and 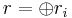 is the adjoint action of
is the adjoint action of  on the complex Lie algebra of a specific subgroup of the Langlands dual group of
on the complex Lie algebra of a specific subgroup of the Langlands dual group of  . When
. When  is the special linear group
is the special linear group 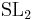 , and
, and 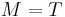 is the maximal torus of diagonal matrices,
is the maximal torus of diagonal matrices,  -factors (
-factors (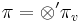 is a character of idèle classes in this situation) are the local factors of Tate's thesis.
is a character of idèle classes in this situation) are the local factors of Tate's thesis.
The  -factors are uniquely characterized by their role in the functional equation and a list of local properties, including multiplicativity with respect to parabolic induction. They satisfy a relationship involving Artin L-functions and Artin root numbers when
-factors are uniquely characterized by their role in the functional equation and a list of local properties, including multiplicativity with respect to parabolic induction. They satisfy a relationship involving Artin L-functions and Artin root numbers when  gives an archimedean local field or when
gives an archimedean local field or when  is non-archimedean and
is non-archimedean and 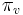 is a constituent of an unramified principal series representation of
is a constituent of an unramified principal series representation of 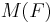 . Local
. Local  -functions and root numbers ε
-functions and root numbers ε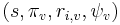 are then defined at every place, including
are then defined at every place, including 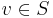 , by means of Langlands classification for
, by means of Langlands classification for  -adic groups. The functional equation takes the form
-adic groups. The functional equation takes the form
are the completed global  -function and root number.
-function and root number.
Examples of automorphic L-functions
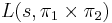 , the Rankin–Selberg
, the Rankin–Selberg  -function of cuspidal automorphic representations
-function of cuspidal automorphic representations 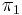 of
of 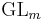 and
and 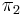 of
of 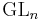 .
.
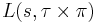 , where
, where  is a cuspidal automorphic representation of
is a cuspidal automorphic representation of 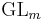 and
and  is a globally generic cuspidal automorphic representation of a classical group
is a globally generic cuspidal automorphic representation of a classical group  .
.
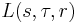 , with
, with  as before and
as before and  a symmetric square, an exterior square, or an Asai representation of the dual group of
a symmetric square, an exterior square, or an Asai representation of the dual group of 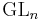 .
.
A full list of Langlands–Shahidi L-functions[4] depends on the quasi-split group  and maximal Levi subgroup
and maximal Levi subgroup  . More specifically, the decomposition of the adjoint action
. More specifically, the decomposition of the adjoint action 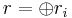 can be classified using Dynkin diagrams.
can be classified using Dynkin diagrams.
Analytic properties of L-functions
Global  -functions are said to be nice[5] if they satisfy:
-functions are said to be nice[5] if they satisfy:
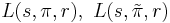 extend to entire functions of the complex variable
extend to entire functions of the complex variable  .
.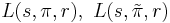 are bounded in vertical strips.
are bounded in vertical strips.- (Functional Equation)
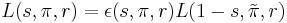 .
.
Langlands–Shahidi  -functions satisfy the functional equation. Progress towards boundedness in vertical strips was made by S. S. Gelbart and F. Shahidi[6]. And, after incorporating twists by highly ramified characters, Langlands–Shahidi
-functions satisfy the functional equation. Progress towards boundedness in vertical strips was made by S. S. Gelbart and F. Shahidi[6]. And, after incorporating twists by highly ramified characters, Langlands–Shahidi  -functions do become entire[7].
-functions do become entire[7].
Another result is the non-vanishing of  -functions. For Rankin–Selberg products of general linear groups it states that
-functions. For Rankin–Selberg products of general linear groups it states that 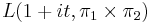 is non-zero for every real number t.
is non-zero for every real number t.
Applications to functoriality and to representation theory of  -adic groups
-adic groups
- Functoriality for the classical groups: A cuspidal globally generic automorphic representation of a classical group admits a Langlands functorial lift to an automorphic representation of
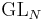 [8], where
[8], where  depends on the classical group. Then, the Ramanujan bounds of W. Luo, Z. Rudnick and P. Sarnak[9] for
depends on the classical group. Then, the Ramanujan bounds of W. Luo, Z. Rudnick and P. Sarnak[9] for 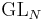 over number fields yield non-trivial bounds for the generalized Ramanujan conjecture of the classical groups.
over number fields yield non-trivial bounds for the generalized Ramanujan conjecture of the classical groups.
- Symmetric powers for
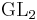 : Proofs of functoriality for the symmetric cube and for the symmetric fourth[10] powers of cuspidal automorphic representations of
: Proofs of functoriality for the symmetric cube and for the symmetric fourth[10] powers of cuspidal automorphic representations of 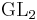 were made possible by the Langlands–Shahidi method. Progress towards higher Symmetric powers leads to the best possible bounds towards the Ramanujan–Peterson conjecture of automorphic cusp forms of
were made possible by the Langlands–Shahidi method. Progress towards higher Symmetric powers leads to the best possible bounds towards the Ramanujan–Peterson conjecture of automorphic cusp forms of 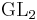 .
.
- Representations of
 -adic groups: Applications involving Harish-Chandra
-adic groups: Applications involving Harish-Chandra  functions (from the Plancherel formula) and to complementary series of
functions (from the Plancherel formula) and to complementary series of  -adic reductive groups are possible. For example,
-adic reductive groups are possible. For example, 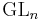 appears as the Siegel Levi subgroup of a classical group G. If
appears as the Siegel Levi subgroup of a classical group G. If  is a smooth irreducible ramified supercuspidal representation of
is a smooth irreducible ramified supercuspidal representation of 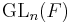 over a field
over a field  of
of  -adic numbers, and
-adic numbers, and 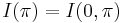 is irreducible, then:
is irreducible, then:
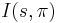 is irreducible and in the complementary series for
is irreducible and in the complementary series for 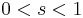 ;
;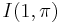 is reducible and has a unique generic non-supercuspidal discrete series subrepresentation;
is reducible and has a unique generic non-supercuspidal discrete series subrepresentation;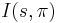 is irreducible and never in the complementary series for
is irreducible and never in the complementary series for 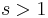 .
.
Here, 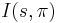 is obtained by unitary parabolic induction from
is obtained by unitary parabolic induction from
-
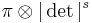 if
if 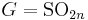 ,
, 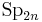 , or
, or 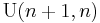 ;
;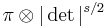 if
if 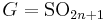 , or
, or 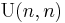 .
.
References
- ^ F. Shahidi, On certain
 -functions, American Journal of Mathematics 103 (1981), 297–355.
-functions, American Journal of Mathematics 103 (1981), 297–355. - ^ R. P. Langlands, On the Functional Equations Satisfied by Eisenstein Series, Lecture Notes in Math., Vol. 544, Springer-Verlag, Berlin-Heidelberg-New York, 1976.
- ^ F. Shahidi, A proof of Langlands conjecture on Plancherel measures; Complementary series for
 -adic groups, Annals of Mathematics 132 (1990), 273–330.
-adic groups, Annals of Mathematics 132 (1990), 273–330. - ^ F. Shahidi, Eisenstein Series and Automorphic
 -functions, Colloquium Publications, Vol. 58, American Mathematical Society, Providence, Rhode Island, 2010.
-functions, Colloquium Publications, Vol. 58, American Mathematical Society, Providence, Rhode Island, 2010. - ^ J. W. Cogdell and I. I. Piatetski–Shapiro, Converse theorems for
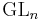 , Publications Mathématiques de l'IHÉS 79 (1994), 157–214.
, Publications Mathématiques de l'IHÉS 79 (1994), 157–214. - ^ S. Gelbart and F. Shahidi, Boundedness of automorphic
 -functions in vertical strips, Journal of the American Mathematical Society, 14 (2001), 79–107.
-functions in vertical strips, Journal of the American Mathematical Society, 14 (2001), 79–107. - ^ H. H. Kim and F. Shahidi, Functorial products for
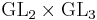 and the symmetric cube for
and the symmetric cube for 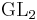 , Annals of Mathematics 155 (2002), 837–893.
, Annals of Mathematics 155 (2002), 837–893. - ^ J. W. Cogdell, H. H. Kim, I. I. Piatetski–Shapiro, and F. Shahidi, Functoriality for the classical groups, Publications Mathématiques de l'IHÉS 99 (2004), 163–233
- ^ W. Luo, Z. Rudnick, and P. Sarnak, On the generalized Ramanujan conjecture for
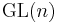 , Proceedings of Symposia in Pure Mathematics 66, part 2 (1999), 301–310.
, Proceedings of Symposia in Pure Mathematics 66, part 2 (1999), 301–310. - ^ H. H. KimFunctoriality for the exterior square of
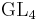 and the symmetric fourth of
and the symmetric fourth of 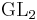 , Journal of the American Mathematical Society 16 (2002), 131–183.
, Journal of the American Mathematical Society 16 (2002), 131–183.